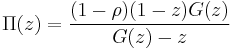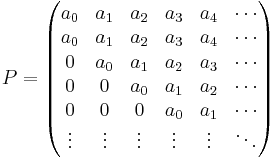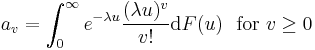M/G/1 queue

In queueing theory, a discipline within the mathematical theory of probability, a M/G/1 queue represents the queue length in a system having a single server, where arrivals are detemined by a Poisson process and job service times can have an arbitrary distribution. The model name is written in Kendall's notation, and is an extension of the M/M/1 queue, where service times must be exponentially distributed. The classic application of the M/G/1 queue is to model performance of a fixed head hard disk.[1]

Contents

Model definition

A queue represented by a M/G/1 queue is a stochastic process whose state space is the set {0,1,2,3...}, where the value corresponds to the number of members in the queue, including any being served. Transitions from state i to i + 1 represent the arrival of a new queue member: the times between such arrivals have an exponential distribution with parameter λ. Transitions from state i to i − 1 represent a member who has been being served, fininshing being served and departing: the length of time required for serving an individual queue member has a general distribution function. The lengths of times between arrivals and of service periods are random variables which are assumed to be statistically independent.

Queue length

The probability generating function of the stationary queue length distribution is given by the Pollaczek–Khinchine transform equation[1]

\Pi(z) = \frac{(1-\rho)(1-z)G(z)}{G(z)-z}

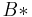where G(z)=B*[\lambda(1-z)] and B* is the Laplace–Stieltjes transform of the service time distribution function. This can be found either using by direct computation or using the method of supplementary variables. The Pollaczek–Khinchine formula gives the mean queue length and mean waiting time in the system.[2][3]

Busy period

The busy period is the time spent in states 1, 2, 3,… between visits to the state 0. The expected length of a busy period is 1/(μ−λ) where μ is the expected length of service time and λ the rate of the Poisson process governing arrivals.[4]

Arrival theorem

As the arrivals are determined by a Poisson process, the arrival theorem holds.

M/G/1 type Markov chains

Consider the embedded Markov chain of the M/G/1 queue, where the time points selected are immediately after departure instants. The customer being served (if there is one) has received zero seconds of service. Between departures, there can be 0, 1, 2, 3,… arrivals. So from state i the chain can move to state i – 1, i, i + 1, i + 2, ….[5] The embedded Markov chain has transition matrix

P = \begin{pmatrix} a_0 & a_1 & a_2 & a_3 & a_4 & \cdots \\ a_0 & a_1 & a_2 & a_3 & a_4 & \cdots \\ 0 & a_0 & a_1 & a_2 & a_3 & \cdots \\ 0 & 0 & a_0 & a_1 & a_2 & \cdots \\ 0 & 0 & 0 & a_0 & a_1 & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{pmatrix}

where

a_v = \int_0^\infty e^{-\lambda u} \frac{(\lambda u)^v}{v!} \text{d}F(u) ~\text{ for } v \geq 0

and F(u) is the service time distribution and λ the Poisson arrival rate of jobs to the queue. Markov chains with generator matrices or block matrices of this form are called M/G/1 type Markov chains.[6]

M/G/k: multiple servers

Results for an extended version of this problem with k > 1 servers remains an open problem.[7] In this model arrivals are determined by a Poisson process and jobs can be served by any one of k servers. Tijms et al believe it is "not likely that computationally tractable methods can be developed to compute the exact numerical values of the steady-state probability in the M/G/k queue."[8]

Various approximations for the average queue size and average delay a job experiences have been offered by different authors.[8]

References

  1. ^ a b Harrison, Peter; Patel, Naresh M. (1992). Performance Modelling of Communication Networks and Computer Architectures. Addison–Wesley. 
  2. ^ Pollaczek, F. (1930). "Über eine Aufgabe der Wahrscheinlichkeitstheorie". Mathematische Zeitschrift 32: 64–100. doi:10.1007/BF01194620. 
  3. ^ Khintchine, A. Y (1932). "Mathematical theory of a stationary queue". Matematicheskii Sbornik 39 (4): 73–84. http://mi.mathnet.ru/rus/msb/v39/i4/p73. Retrieved 2011-07-14. 
  4. ^ Ross, Sheldon M.; Seshadri, Sridhar (1999). "Hitting time in an M/G/1 queue". Journal of Applied Probability: 934–940. JSTOR 3215453. http://pages.stern.nyu.edu/~sseshadr/journalArticles/hitting_time_in_mg1_queue.pdf. 
  5. ^ Stewart, William J. (2009). Probability, Markov chains, queues, and simulation. Princeton University Press. p. 510. ISBN 0691140626. 
  6. ^ Neuts, Marcel F. (1981). Matrix-geometric solutions in stochastic models: an algorithmic approach (Johns Hopkins Studies in Mathematical Sciences). Johns Hopkins University Press. p. 2. ISBN 0486683427. 
  7. ^ Kingman, J. F. C. (2009). "The first Erlang century—and the next". Queueing Systems 63: 3–4. doi:10.1007/s11134-009-9147-4.  edit
  8. ^ a b Tijms, H. C.; Van Hoorn, M. H.; Federgruen, A. (1981). "Approximations for the Steady-State Probabilities in the M/G/c Queue". Advances in Applied Probability 13 (1): 186–206. doi:10.2307/1426474.  edit